Annexes

Annexe I. Systèmes de chiffrement

Un système de chiffrement est dit symétrique quand il utilise la même clé pour chiffrer et déchiffrer. Il est asymétrique quand il utilise des clés différentes : une paire composée d'une clé publique, servant au chiffrement, et d'une clé privée, servant à déchiffrer.

1. Chiffrement symétrique

La cryptographie symétrique, également dite à clef secrète (par opposition à la cryptographie à clef publique), est la plus ancienne forme de chiffrement. Une des plus anciennes — bien que célèbre — formes connues est le « Chiffre de César ». Des traces plus anciennes de son utilisation chez les Égyptiens remontent vers 2000 avant J.C.

L'un des concepts fondamentaux de la cryptographie symétrique est la clef, qui est une information devant permettre de chiffrer et de déchiffrer un message et à laquelle doit se réduire la sécurité de la communication. On parle ainsi de secret partagé dans le cadre d'échanges protégés par chiffrement symétrique ; le secret — et donc la sûreté — réside dans la clef. Auguste Kerckhoffs (La cryptographie militaire, 1883) est certainement l'un des premiers à avoir pleinement compris cela : pour espérer être sûr, l'algorithme doit pouvoir être divulgué. C'est ce que l'on appelle désormais le principe de Kerckhoffs.

Il faut ajouter que cette clef doit pouvoir prendre suffisamment de valeurs pour qu'une attaque exhaustive — essai systématique de toutes les clefs — ne puisse être menée à bien car trop longue. On parle de sécurité calculatoire.

Jusqu'aux communications numériques, les systèmes utilisaient l'alphabet et combinaient les substitutions — les symboles sont changés mais restent à leur place —, et les transpositions — les symboles ne sont pas modifiés mais changent de place.

Depuis l'avènement du numérique, les paradigmes du chiffrement symétrique ont bien changé. D'une part, la discipline s'est formalisée, même si la conception de système de chiffrement garde inévitablement un aspect artisanal. En effet dans ce domaine, la seule chose que l'on sache prouver est la résistance face à des types d'attaques connues, pour les autres ... D'autre part, la forme du texte chiffre ayant changé, les méthodes ont suivi. Les algorithmes modernes chiffrent des suites de bits.

On distingue deux types d'algorithmes, les algorithmes en blocs, qui prennent n bits en entrée et en ressortent n, et les algorithmes à flots, qui chiffrent bit par bit sur le modèle du chiffre de Vernam. Dans ce dernier cas, l'algorithme engendre une suite de bits qui est ajouté à l'aide d'un OU exclusif ¹¹ (XOR) à la suite binaire à chiffrer.

La seconde famille d'algorithmes, ceux en blocs, sont en général construits sur un modèle itératif. Ce modèle utilise une fonction 'F qui prend une clef k et un message de 'n' bits. C'est cette fonction 'F qui est itérée un certain nombre de fois, on parle de nombre de tour, ou de rondes. À chaque tour, la clef k utilisée est changée et le message que l'on chiffre est le résultat de l'itération précédente. C'est sur ce modèle que fonctionne l'algorithme TEA.

Principe des rondes

2. Chiffrement asymétrique

La cryptographie asymétrique, ou cryptographie à clé publique est fondée sur l'existence de fonctions à sens unique — c'est-à-dire qu'il est simple d'appliquer cette fonction à un message, mais extrêmement difficile de retrouver ce message à partir du moment où on l'a transformé.

En réalité, on utilise en cryptographie asymétrique des fonctions à sens unique et à brèche secrète. Une telle fonction est difficile à inverser, à moins de posséder une information particulière, tenue secrète, nommée clé privée.

On parle de clé publique pour la fonction qu'on diffuse (sans avoir à se préoccuper de sa sécurité) et de clé privée pour l'information secrète (qui doit rester la propriété exclusive du destinataire des messages). Ainsi, n'importe qui pourra chiffrer des messages avec cette clé publique, et seul le détenteur de la clef privée pourra les déchiffrer.

D'autre part, l'utilisation par son détenteur de la clef privée sur le message (ou, en pratique, sur son condensat), permettra à n'importe qui de vérifier, en appliquant au résultat la clé publique (et en retrouvant donc ce message — ou son condensat) que nulle autre n'a pu signer ce message.

3. Chiffrement TEA et xTEA

L'algorithme de chiffrement TEA (de l'anglais « Tiny Encryption Algorithm » est un système de cryptographie symétrique par bloc développée par David Wheeler et Roger Needham, de l'université de Cambridge, placé dans le domaine public.

Il fonctionne en utilisant des opérations algébriques (XOR, ADD, et SHIFT) permettant d'obtenir une bonne diffusion sans nécessiter de « boîtes noires » telles des « S-boxes » et des « P-boxes », et chiffre des blocs de 64 bits d'information à l'aide d'une clef de 128 bits. Cela permet une grande rapidité sur les ordinateurs actuels, qui effectuent très vite ces opérations. Java est aussi efficace pour ces opérations sur d'autre types d'architecture, pour diverses raisons telle la non-promotion des types « byte » en « int » après de nombreux ADD.

David Wagner, John Kelsey, et Bruce Schneier ont publié un article à propos d'une attaque sur la clef nécessitant 223 textes clairs choisis et leur résultat. Cette attaque est rendue possible par le simple enchaînement des clefs, même si elle n'est pas vraiment utilisable en pratique.

Une version améliorée de TEA, non sensible à cette attaque, a depuis été proposée par les auteurs originaux, sous le nom de xTEA.

L'algorithme est néanmoins considéré comme très sûr, et aucune cryptanalyse connue n'a pu être utilisée contre lui. Il peut être considéré aussi sûr qu'IDEA, sans souffrir de ses problèmes de licence.

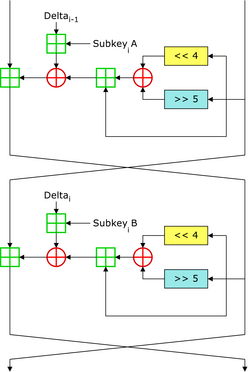
Figure 16 : Une ronde de l'algorithme xTEA

Annexe II. Diagramme des classes

La Figure 17 présente le diagramme des classes qui ont été écrites spécifiquement pour le projet